ASCII
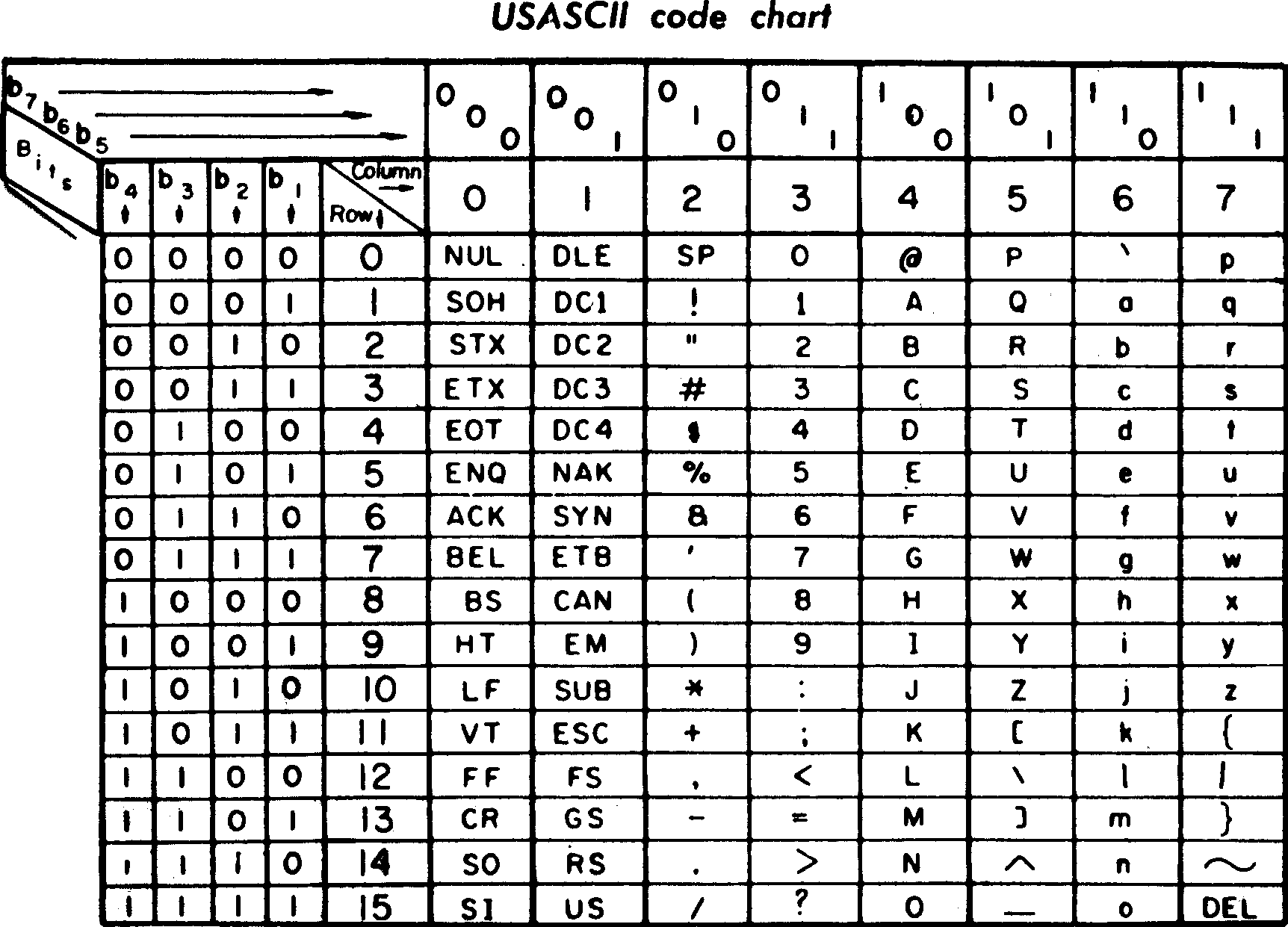
American Standard Code for Information Interchange
- Représentation des caractères (pour l'anglais) sur 7 bits
- Développée dans les années 1960, révisée jusqu'en 1986
1h cours (7 semaines) + 3h TD (6 semaines)
Contenu :
Un bit (binary digit) est une unité d'information qui représente un état logique pouvant prendre deux valeurs (souvent notées \(0\) et \(1\)).

American Standard Code for Information Interchange
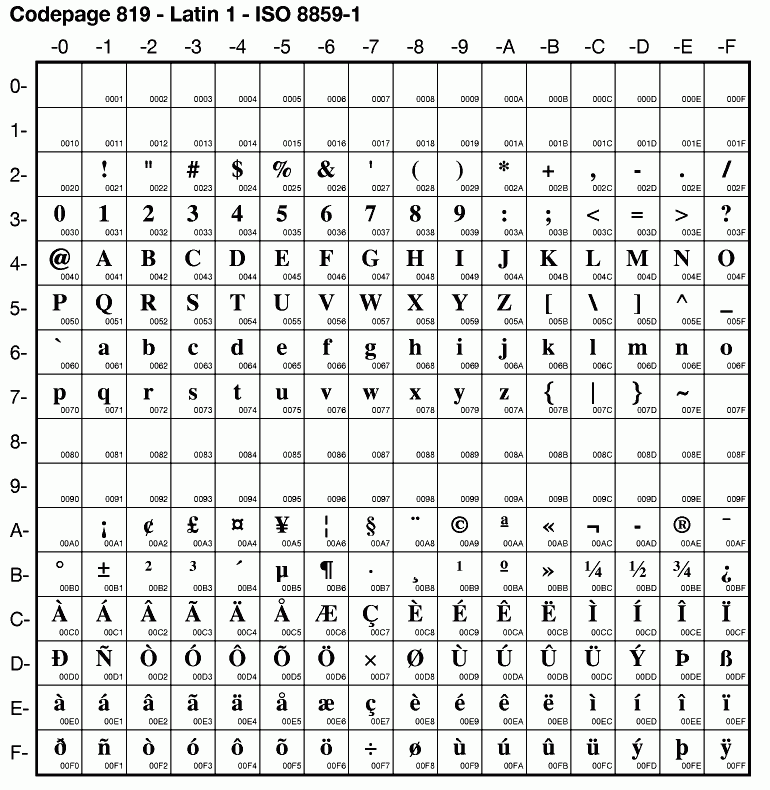
La table a depuis été étendue de différentes manières pour ajouter des caractères supplémentaires
En pratique on considère les bits par groupes de 8 :
Pour les grandes valeurs, on utilise des unités multiples de l'octet
Historiquement :
Depuis 1998 :
Si l'alphabet est simple, on peut utiliser un format ASCII (p.ex. ISO-latin-9 pour le français)
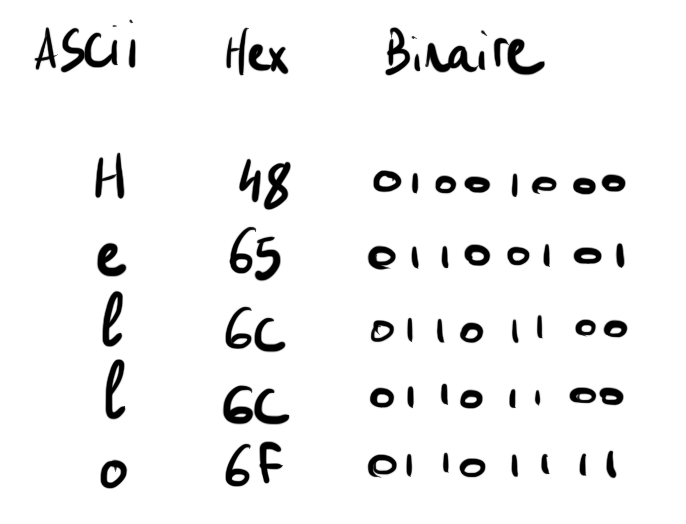
Si on veut utiliser un alphabet plus large, on peut utiliser l'Unicode
Il existe plusieurs encodages Unicode :
0xxxxxxx110xxxxx 10xxxxxx1110xxxx 10xxxxxx 10xxxxxx11110xxx 10xxxxxx 10xxxxxx 10xxxxxxAttention ! L'encodage doit être connu pour éviter les problèmes

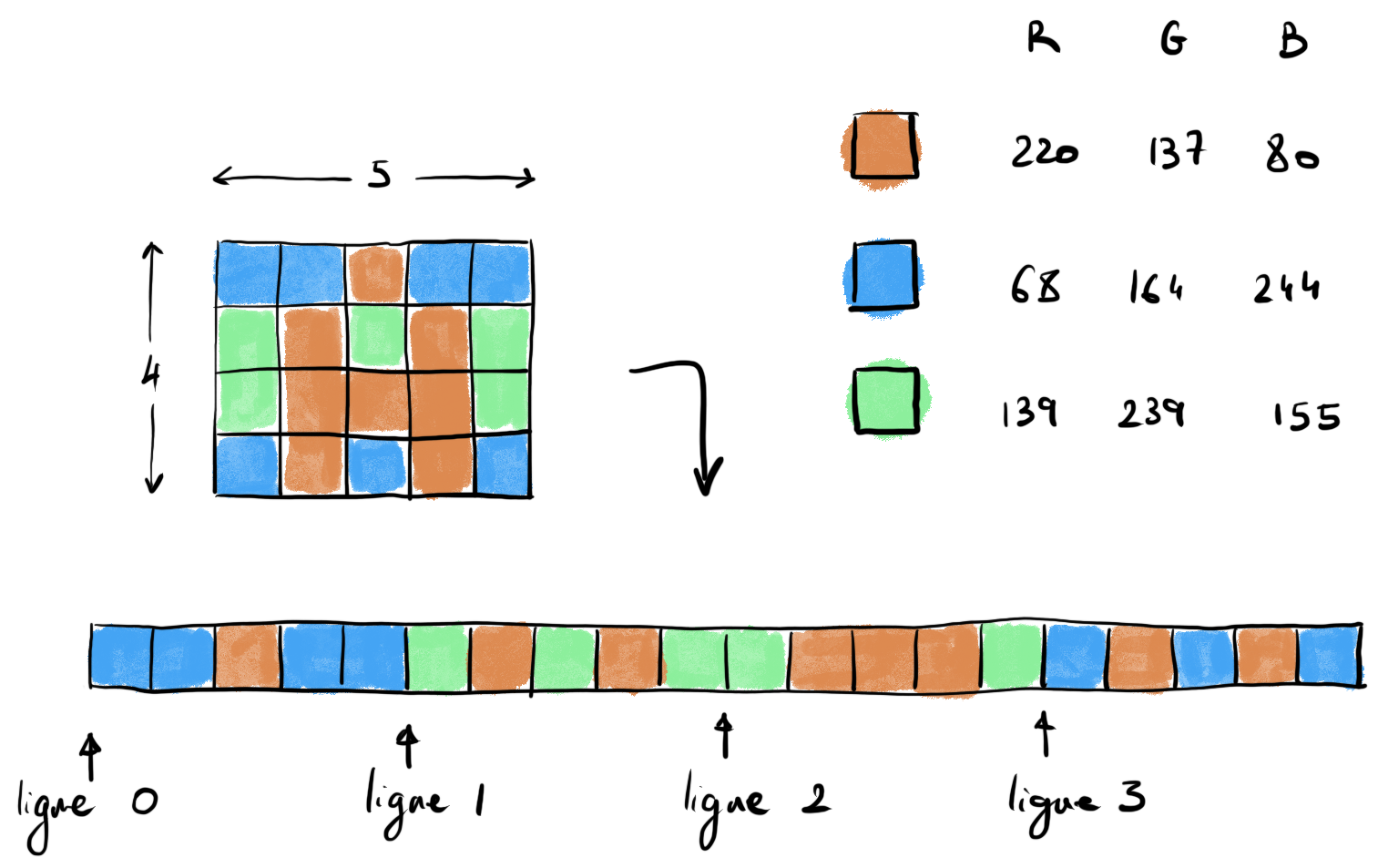
Pour représenter une image, on peut décrire chacun de ses pixels
Pour une image en couleurs de \(n \times m\) pixels :
→ \(3\times n\times m\) octets pour représenter l'image
(3 Mo pour une image 1000x1000)
Pour représenter une fonction continue (p.ex. piste audio)
Taille d'un fichier audio (en octets) :
Environ 10Mo par minute pour un fichier wave en stereo, 44.1 kHz, 16 bits par échantillon.
Un signal audio peut être décomposé en une superposition de signaux sinusoïdaux
On considère que l'oreille humaine perçoit les fréquences jusqu'à 20 kHz
→ Un échantillonage de 44.1 kHz permet d'enregistrer les fréquences audibles
→ Il faut au moins \(3\times n\times m\) octets
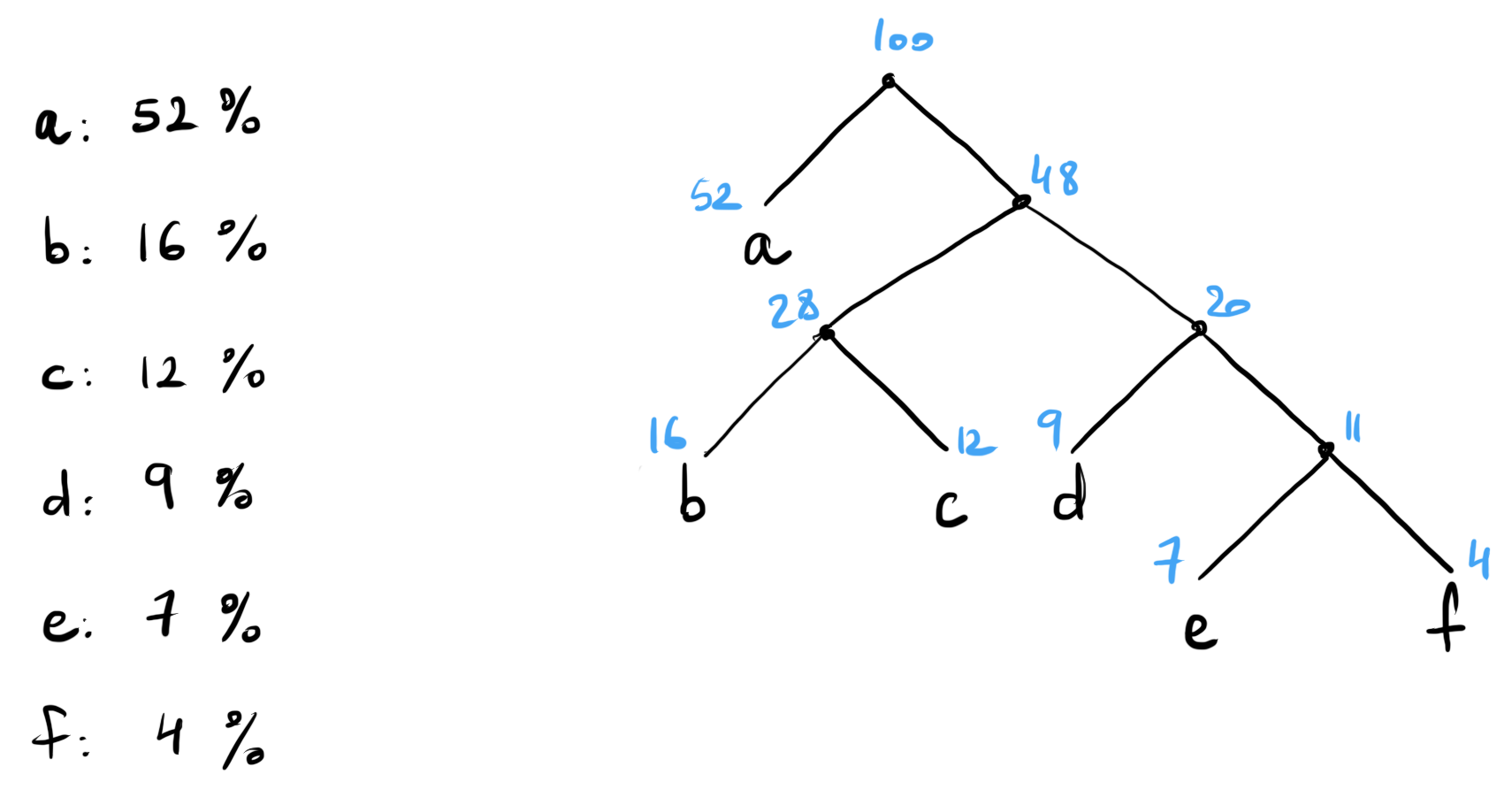

Si toutes les valeurs n'ont pas la même fréquence on peut représenter les plus fréquentes sur moins de bits
→ Longueur moyenne d'un message est plus petite qu'avec un code de taille fixe