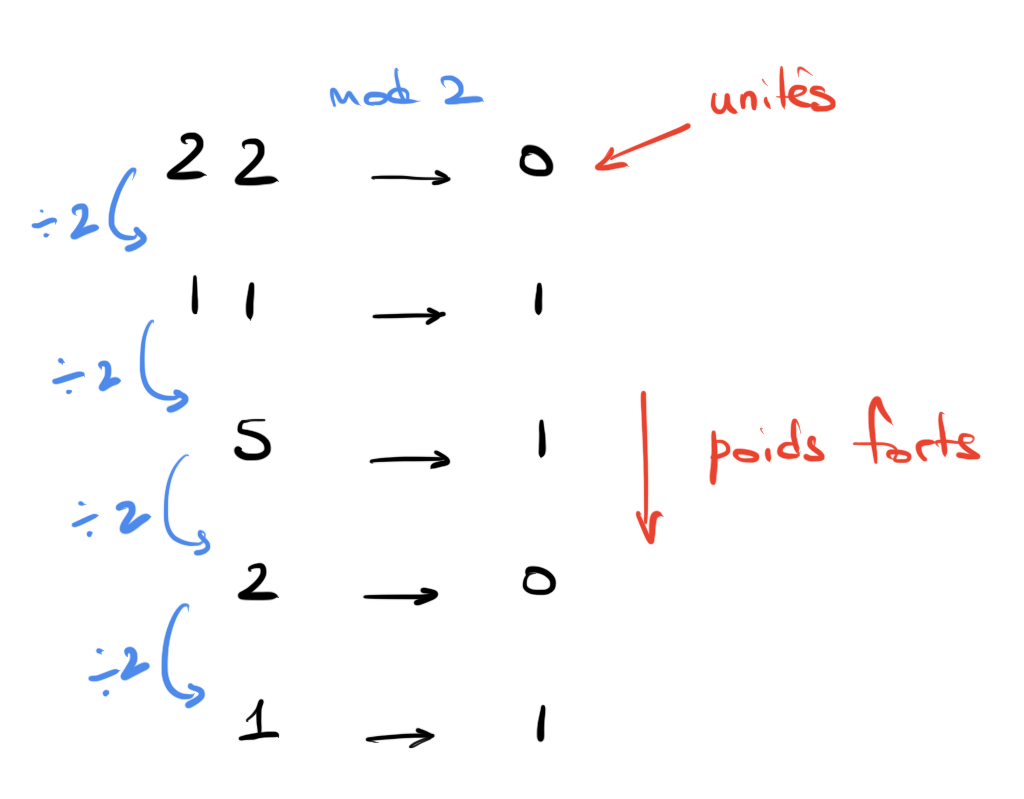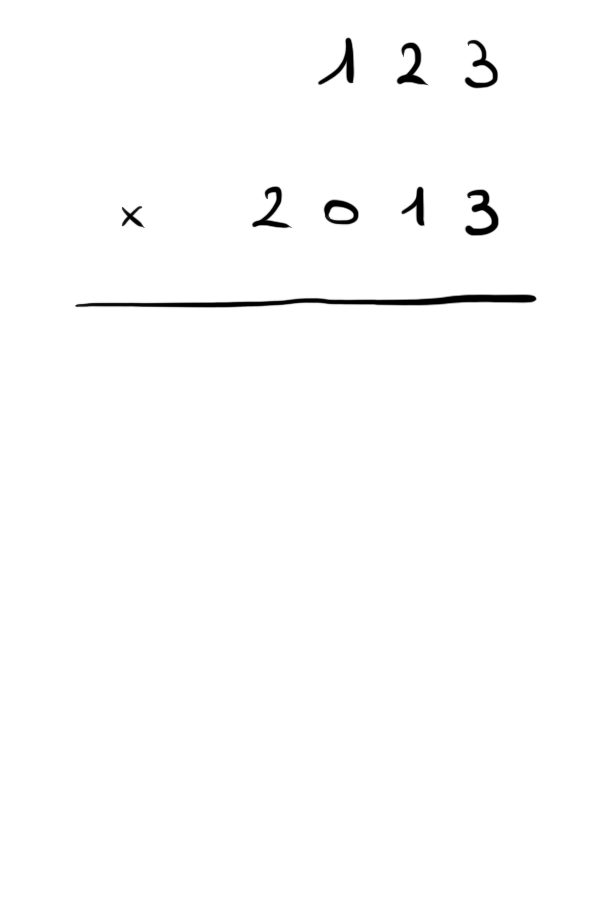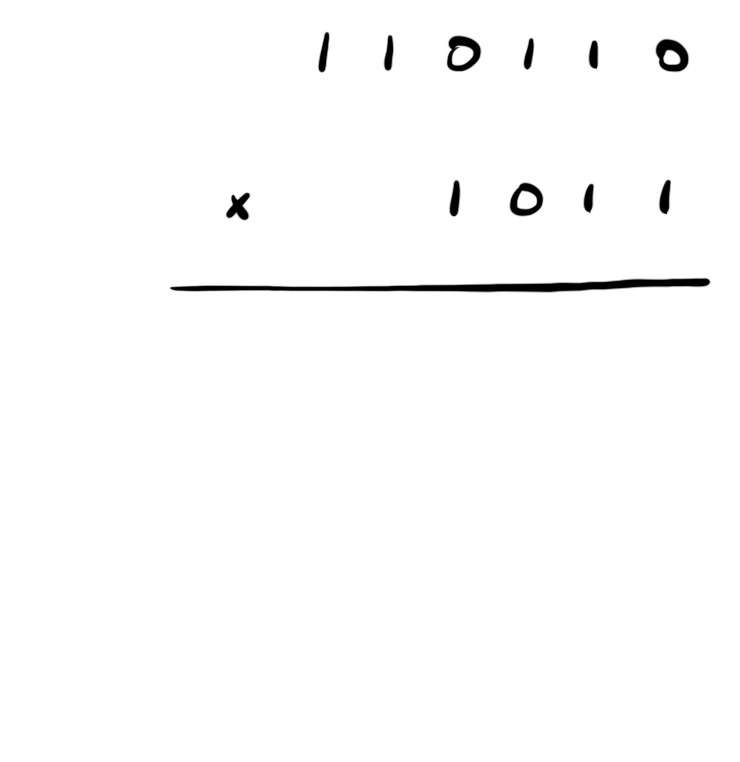Écriture décimale

Image : Les maths avec Léonie (CE1)

Représentation « usuelle » des nombres

10 chiffres ("0", "1", ..., "9")
valeur d'un chiffre dépend de sa position (unités, dizaines, centaines, etc.)
permet de représenter tous les entiers
écriture unique (si on enlève les 0 initiaux)

Écriture en base quelconque

Ex. en base 5 :

chiffres : 01234
$324_5$ →
$3\times 5^2 + 2\times 5 + 4\times 1$

Ex. en base 2 (binaire):

chiffres : 01
$1011_2$ →
$1\times 2^3 + 0\times 2^2 + 1\times 2 + 1\times 1$

Ex. en base 16 (hexadécimal) :

chiffres : 0123456789ABCDEF
$3FB_{16}$ →
$3\times 16^2 + 15\times 16 + 11\times 1$

10 n'est pas particulier, on peut choisir une autre base $b > 1$

$b$ chiffres
chaque position vaut $b$ fois plus que celle de droite
$c_nc_{n-1}\ldots c_1c_0 = \sum\limits^n_{k=0} c_kb^k$

Incrémentation

En base 3 :

...

1012221

1012222
1020000

1020001

...

En base 2 :

0
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
...

Pour incrémenter (ajouter 1)

remplacer tous les chiffres $(b-1)$ de la fin par des 0
incrémenter le chiffre le plus à droite $\neq (b-1)$

Avec $k$ chiffres on peut compter jusqu'à $(b^k-1)$

Conversions (1)

$432_5$ → $4\times 5^2 + 3\times 5 + 2\times 1$

$$\begin{aligned}327 &= 2 \times 125 + 77\\ &= 2 \times 125 + 3 \times 25 + 2\\ &= 2 \times 125 + 3 \times 25 + 0\times 5 + 2\\ \end{aligned}$$

$→ 2302_5$

Observation :

Unicité de la décomposition $$x = \sum\limits^n_{k=0} c_kb^k$$

Décodage (base $b$ → base 10):

Multiplier chaque chiffre par la puissance de $b$ correspondante
Ajouter

Encodage (base 10 → base $b$):

Insertion de la plus grande puissance de $b$ ≤ $x$
On cherche combien de fois on peut mettre cette puissance

Attention : si une puissance n'apparaît pas il faut ajouter un 0

Conversions (2)

→ $22_{10} = 10110_2$

100110 100110 100110 100110 100110 100110 100110

$t = 0$

$t = 1$ ($\times 2 + 1$)

$t = 2$ ($\times 2$)

$t = 4$ ($\times 2$)

$t = 9$ ($\times 2 + 1$)

$t = 19$ ($\times 2 + 1$)

$t = 38$ ($\times 2$)

Observations :

Ajouter un zéro ↔ multiplier par $b$
Ajouter chiffre $c$ ↔ $\times b + c$

Encodage (base 10 → base $b$):

Chiffre des unités est $x\mod b$
On divise par $b$ pour trouver les autres chiffres

Décodage (base $b$ → base 10):

$t ← 0$
Pour chaque chiffre $c$ (depuis la gauche) $$t← bt + c$$

Addition

Ex. en base 5

Pour additionner des nombres en base $b$

Aligner les chiffres à droite (unités)
Ajouter les chiffres depuis la droite
En cas de dépassement, on transfère $d$ sur la colonne de gauche (retenue)

Soustraction

Ex. en base 4

Pour soustraire des nombres en base $b$

Aligner les chiffres à droite (unités)
Soustraire les chiffres depuis la droite
En cas de dépassement, on transfère $d$ depuis la colonne de gauche (retenue)

Multiplication

Ex. en base 4

Ex. en base 2

Pour multiplier des nombres en base $b$

Aligner les chiffres à droite (unités)
Multiplier un des nombres par les chiffres du second (avec décalage)
Ajouter les résultats

Nombres à virgule

Pour représenter des nombres non-entiers

On ajoute des chiffres de poids $$\frac{1}{b}, \frac{1}{b^2}, \frac{1}{b^3}, \ldots$$
Pour reconnaître la position des unités on ajoute une virgule

Pour représenter un nombre non entier en base $b$ :

On représente la partie entière
Pour la partie fractionnaire ($0≤f<1$)
- On multiplie par $2$
- Si $≥ 1$ → $1$, sinon $0$
- On ignore la partie entière
- Si une valeur se répète l'écriture est périodique

Nombres à virgules

Quelques propriétés :

Avec des développements infinis, on peut représenter tous les nombres réels (certains réels ont deux représentations)
Les nombres rationnels sont exactement ceux qui ont une représentation ultimement périodique
Un nombre qui a une écriture finie en base $b_1$ n'a pas nécessairement une écriture finie en base $b_2$ (p. ex. : $0,1_3 = 0,3333\ldots_{10}$)
Si $p \wedge q = 1$, $\frac{p}{q}$ a une écriture finie en base $b$ si et seulement si tous les facteurs premiers de $q$ sont des diviseurs de $b$

Cours n°2 :
Représentation des nombres

Notation positionnelle

Écriture décimale

Écriture en base quelconque

Incrémentation

Conversions (1)

Conversions (2)

Arithmétique

Addition

Soustraction

Multiplication

Nombres à virgule

Nombres à virgules

Cours n°2 :Représentation des nombres

Notation positionnelle

Écriture décimale

Écriture en base quelconque

Incrémentation

Conversions (1)

Conversions (2)

Arithmétique

Addition

Soustraction

Multiplication

Nombres à virgule

Nombres à virgules

Cours n°2 :
Représentation des nombres