\(
\newcommand{\llbracket}{[\![}
\newcommand{\rrbracket}{]\!]}
\newcommand{\er}{e_{\operatorname{reel}}}
\newcommand{\eb}{e_{\operatorname{biais}}}
\)
Cours n°4 :
IEEE 754
R1.03 - Intro. Archi
Victor Poupet
2025-12-01
Nombres à virgule
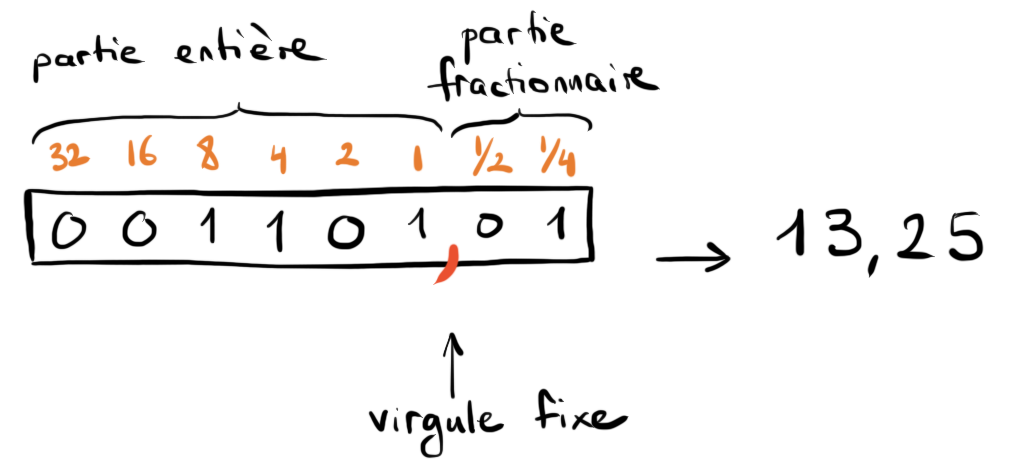
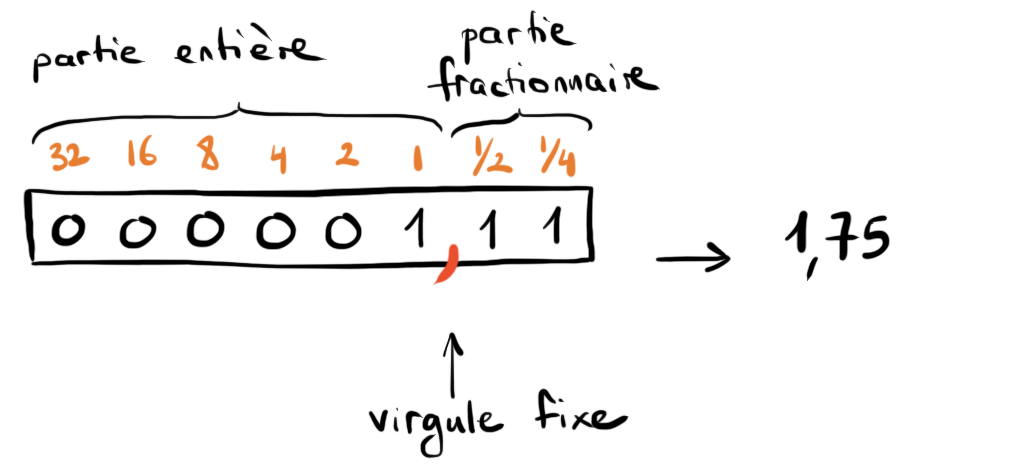
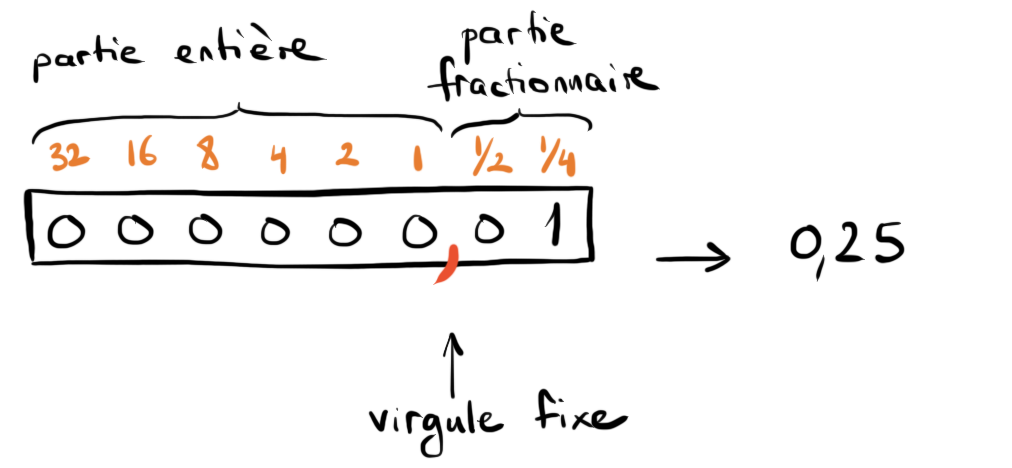
Pour représenter des nombres à virgule, on peut associer des poids fractionnaires à certaines positions
Nombre de bits fixés
Poids fixés
→ virgule fixe
Problème 1 : Perte de précision si l'ordre de grandeur change
Problème 2 : Intervalle réduit
Virgule flottante
Idée : Représenter séparément la valeur et la position de la virgule
→ Virgule flottante
Notation scientifique (base \(b\)): $$ x = ±y \times b^e$$
avec
\(1 ≤ y < b\)
\(e \in \mathbb{Z}\)
Exemples (base 10) :
\(\begin{align}121 &= 1,21 \times 10^2\\
-5640000 &= -5,64 \times 10^6\\
45,1 &= 4,51 \times 10^1\\
-0,000000123 &= -1,23 \times 10^{-7}\\
6,43 &= 6,43 \times 10^0
\end{align}\)
→ Même précision quel que soit l'ordre de grandeur
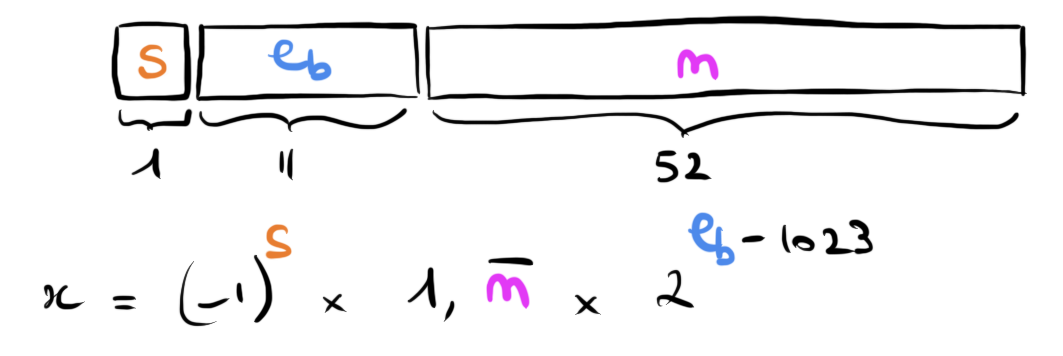
Schéma
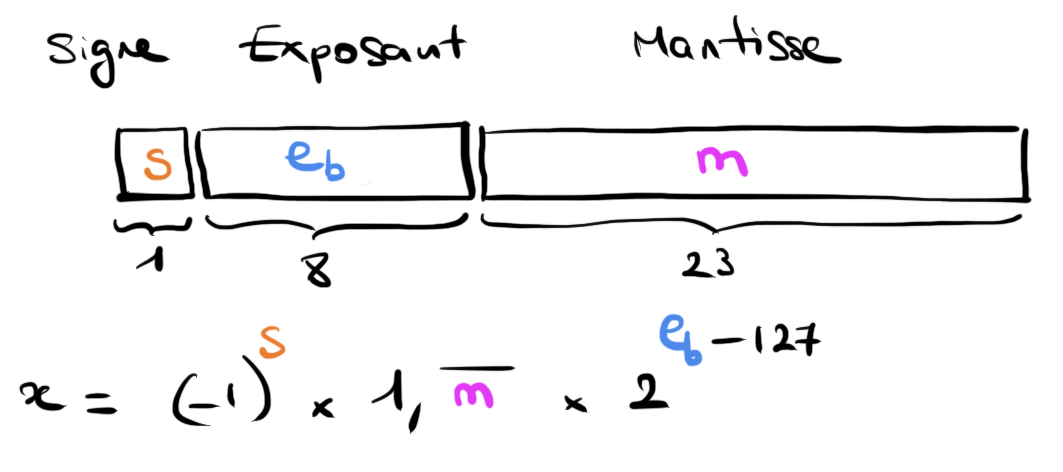
Éléments de la représentation en virgule flottante :
Signe (s)
Exposant (e)
Mantisse (m)
Valeur représentée : $$x = (-1)^s\times m\times 2^e$$
Signe
Le signe d'un nombre à virgule flottante
dans la mantisse ?
séparément (bit de signe) ? ← solution choisie
Le signe est encodé par le premier bit (comme pour les entiers)
0 si positif
1 si négatif
Exposant
L'exposant peut être positif ou négatif
Représentations possibles :
Signe / magnitude
Complément à 1 ou à 2
Repr. biaisée ← solution choisie
Pour faciliter les comparaisons, on choisit une représentation croissante
Exposant donne l'ordre de grandeur
Solution :
Décalage pour éviter les valeurs négatives
Sur \(n\) bits, $$\eb = \er + 2^{n-1} - 1$$
$$\begin{align}-2^{n-1} + 1 &\leq \er \leq 2^{n-1} \\
0 &\leq \eb \leq 2^{n}-1
\end{align}$$
Sur \(8\) bits, $$\eb = \er + 127$$
$$\begin{align}-127 &\leq \er \leq 128 \\
0 &\leq \eb \leq 255
\end{align}$$
Mantisse
Signe codé séparément, donc codage binaire de la valeur absolue
Dans le cas général $$1 ≤ m < 2$$ $$m = 1, \ldots$$
Il n'est pas nécessaire d'indiquer le \(1\) initial (1 implicite )
Par exemple, pour représenter \(12.75\) :
\(12,75_{10} = 1100,11_{2}\)
\(m = {\color{red}1},{\color{blue}10011}\)
On écrit \(\color{blue}1001100\ldots\)
Norme IEEE 754
IEEE Standard for Floating-Point Arithmetic (1985)
Fixe la représentation des nombres
Corrige plusieurs problèmes liés aux implémentations précédentes
Définit le comportement en cas d'exception (division par zéro, dépassement de capacité, etc.)
Définit les règles d'arrondi pour les opérations
Norme IEEE 754
Simple précision (32 bits)
1 bit de signe
8 bits d'exposant biaisé à 127
23 bits de mantisse
Double précision (64 bits)
1 bit de signe
11 bits d'exposant biaisé à 1023
52 bits de mantisse
Norme IEEE 754
IEEE 754 définit deux représentations différentes pour chaque format :
Représentation normalisée
Représentation non normalisée (exceptions)
Représentation normalisée
\(000\ldots 00 < e_b < 111\ldots 11\)
En simple précision
plus petit nombre représentable : \(1,0 \times 2^{-126}\)
plus grand nombre représentable : \(1,111\ldots 1 \times 2^{127} ≈ 2^{128}\)
Exemple
Considérons $$x = -73,25_{10}$$
Signe ? négatif → \(1\)
Représentation binaire de \(|x|\) $$1001001,01$$
Notation scientifique $$1,00100101 \times 2^6$$
Mantisse sur 23 bits (\(1\) implicite)$$001001010000\ldots 0$$
Décalage de l'exposant $$\eb = \er + 127 = 133$$
Exposant biaisé en binaire (8 bits) $$10000101$$
→ Représentation de -73,25 en simple précision :$$1\ 10000101\ 001001010000\ldots 0$$
Représentations non-normalisées
Il existe 3 types de représentations non-normalisées
Représentation dénormalisée
Représentation des infinis (\(±\infty\))
Représentation des exceptions : Not a Number (NaN)
Représentation dénormalisée
Champ de l'exposant ne contient que des 0
Exposant réel vaut \(-2^{|E|-1}+2\) (ex: -126 en SP)
Mantisse n'a pas de \(1\) implicite : \(0 \leq m < 1\)
Valeur représentée
\(x = (-1)^s \times 0,\overline{m} \times 2^{-126}\)(en SP)
\(x = (-1)^s \times 0,\overline{m} \times 2^{-1022}\)(en DP)
Représentation dénormalisée
Importance de la représentation dénormalisée :
Permet de représenter zéro : \(000000\ldots 0\) ou \(100000\ldots 0\)
Plus petit nombre dénormalisé (> 0) : \(0,0000\ldots 01 \times 2^{-126} = 2^{-149}\) (en SP)
La différence de 2 nombres distincts est toujours non-nulle
Plus grand nombre dénormalisé : \(0,11\ldots 11 \times 2^{-126} ≈ 2^{-126}\) (en SP)
(Rappel) plus petit nombre normalisé : \(1,0\times 2^{-126}\) (en SP)
Infini
La représentation correspond à un infini si
le champ de l'exposant ne contient que des 1
le champ de la mantisse ne contient que des 0
$$\begin{align}0\ 11111111\ 00000000000000000000000 &\rightarrow +\infty\\
1\ 11111111\ 00000000000000000000000 &\rightarrow -\infty\\
\end{align}$$
Not a Number
La représentation correspond à Not a Number (NaN) si
le champ de l'exposant ne contient que des 1
le champ de la mantisse contient au moins un 1
Exemples :$$\begin{align}0\ 11111111\ 00000000110001101000000 &\rightarrow \operatorname{NaN}\\
1\ 11111111\ 01101100001000010110000 &\rightarrow \operatorname{NaN}\\
\end{align}$$
Ne correspond pas à une valeur numérique
On ne peut pas effectuer d'opération arithmétique avec NaN (produit toujours NaN)
Résultat des opérations indéfinies (division par 0, \(\infty / \infty\), etc.)
Bilan
Type
Exposant
Mantisse
Zéro
\(0\)
\(0\)
Nombre dénormalisé
\(0\)
\(\neq 0\)
Nombre normalisé
\(1\) à \(2^{|E|}-2\)
quelconque
Infinis
\(2^{|E|} - 1\)
\(0\)
NaN
\(2^{|E|} - 1\)
\(\neq 0\)
Simple précision
\(|E| = 8\)
\(2^{|E|} = 256\)
Double précision
\(|E| = 11\)
\(2^{|E|} = 2048\)
Addition / Soustraction
Pour additionner (ou soustraire) deux nombres en IEEE 754
Restaurer le bit de poids fort (1 implicite)
Décaler les mantisses pour représenter au même exposant
Additionner (ou soustraire) les mantisses
Renormaliser le résultat (nouvel exposant, 1 implicite, arrondi)
\(0.5 + (-0.375)\)
\(\begin{eqnarray}0.5 &\rightarrow& 1.0 \times 2^{-1}\\
-0.375 &\rightarrow& -1.1 \times 2^{-2}\\
\end{eqnarray}\)
\(1.0 \times 2^{-1} + (-0.11) \times 2^{-1}\)
\( = 0.01 \times 2^{-1}\)
\( = 1.0 \times 2^{-4}\)
Multiplication
La multiplication est légèrement plus simple
Calculer le signe du résultat
Ajouter les exposants (réels)
Restaurer le bit de poids fort
Effectuer la multiplication des mantisses
Arrondir, réajuster l'exposant et renormaliser
Arrondis
IEEE 754 définit 4 modes d'arrondis :
Au plus proche (mode par défaut) : arrondir vers la valeur la plus proche, en préférant un nombre pair (LSB=0) si égale distance (round half to even ou banker's rounding )
Vers moins l'infini
Vers plus l'infini
Vers zéro
Les opérations arithmétiques et beaucoup de fonctions élémentaires (log, racines, trigonométrie, etc.) sont calculées avec des arrondis corrects .